Detecting- Incompleteness, Ambiguity,Contradictions and Redundancy in decision table specification

By -

Detecting- Incompleteness, Ambiguity,Contradictions & Redundancy in decision table specification

LOGICAL CORRECTNESS OF DECISION TABLE (CONTD)

A decision table with 1 condition should have 2 elementary rules, each elementary rule must be distinct, each elementary rule must have distinct action, if a decision table with k conditions does not have 2k  rules specified it is said to be incomplete.

For example : DT2 does not have the elementary rule C1:N, C2:N. It is thus incomplete.

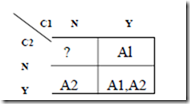
If the decision table has the same elementary rule occurring more than once it is said to have multiplicity of specifications For Example: In DT2 The rule C1:Y,C2:Y occurs twice. Thus it has multiplicity of specification.

If action specified for multiple identical rules are different then it is called ambiguous specifications DT2 has an ambiguity. Rules R11 and R22 are identical but have different actions. Ambiguity may be apparent or real. It is said to be apparent if the rule leading to the ambiguity is logically impossible For example,(x>60)=Y and (x<40)=Y cannot occur simultaneously. Thus in DT2 rules R11 and R22 are apparently ambiguous rules Apparently ambiguous rules is not an error If an apparently ambiguous specification is real then it is a contradiction For example : If C1:(X > 60) = Y and C2:(X > 40) = Y then X = 70 will satisfy both inequalities.

As two actions are specified for (Cl = Y, C2 = Y) and they are different the rule is really ambiguous and is called Contradictory Specification.

If all 2k elementary rules are not present in a k condition decision table is said to be incomplete.

DT2 is incomplete as rule C1:N, C2:N is missing
Rule C1=N, C2:=N is logically possible as C1=N is X<=60
and C2=N is X >= 40. A value of X = 50 will make C1=N,C2=N
Thus DT2 has a real incomplete specification

A decision table which has no real ambiguities or real incompleteness is said to be logically correct. Decision table with logical errors should be corrected

USE OF KARNAUGH MAPS

KARNAUGH map abbreviated K-map is a 2 dimensional diagram with one square per elementary rule

The k-map of DT2 is

image

If more than one action is in one square it is an ambiguous rule

If a square is empty it signifies incomplete specification.

USE OF KARNAUGH MAPS

Structured English procedure:

image

Observe that the fact that the specification is incomplete is obvious in the Decision table whereas the structured English specification seems complete which is not.

DT4: DECISION TABLE-ARREARS MANAGEMENT

image

image

CORRECT DECISION TABLE

If users say that for rules C1C2C3C4:NYNY AND YYNY (marked with + in k-map) the action is A4 and for C1C2C3C4:NNNN also it is A4, the corrected map is

image

Question: Can the number of rules be reduced?
Answer : Yes, by combining rules with the same action
Action A1 can be represented by the Boolean expression:
C1C2C3C4 + C1C2C3C4 + C1C2C3C4 = C1C2C3C4 + C1C2C3 (C4+C4) =C1C2C3C4+C1C2C3 = C1C2C4 + C1C2C3

Comments

Post a Comment

Popular posts from this blog

WORKED EXAMPLES ON PROCESS SPECIFICATION.

By -
Image
PROCESS SPECIFICATION WORKED EXAMPLES 6.1 A bank has the following policy on deposits: On deposits of Rs. 5000 and above and for three years or above the interest is 12%. On the same deposit for a period less than 3 years it is 10%. On deposits below Rs. 5000 the interest is 8% regardless of the period of deposit. Write the above process using (i) Structured English (ii) A decision table 6.2 An organization maintains an employee file in which each record has following data: { Employee No., employee name, employee gross pay}. It has been decided to increase the pay as per the following formula: For pay of Rs. 1000 or less increase 15%. For pay of more than Rs. 1000 but up to Rs. 2500 increase 10%. For pay over Rs. 2500 increase 5%. (i) Writ e a structured English processing rule corresponding to the above policies. (ii) Express the policies as a decision table. (i) While employee records left in file do Read Number, name , gross pay 6.3 An offshore gas company bills it
Read more

Why do we need information systems, management structure, requirements of information at different levels of management.

By -
Image
Why do we need information systems, management structure, requirements of information at different levels of management NEED FOR INFORMATION SYSTEMS Information systems are needed when timely processing for fast action is needed, same data has to be processed in different ways and when organizations require innovative processing. MANAGEMENT STRUCTURE Functional areas of management are as follows: •PRODUCTION • MARKETING • MATERIALS – purchase, stores • FINANCE –Accounts • HUMAN RESOURCE DEVELOPMENT(HRD) • RESEARCH AND DEVELOPMENT (R&D) INFORMATION FOR MANAGEMENT A Production Management The following type of information is needed in production management: Strategic Information: 1)Yearly and monthly production quotas and alternate schedules 2)Policies on machine replacement, augmentation and modernization. 3)Identifying best product mix. Tactical Information 1)Identifying and controlling areas of high cost. 2) Identifying critical bottlenecks in production. 3)
Read more

The User Interface:Establishing User Interfaces

By -
Image
The User Interface Establishing User Interfaces The success factors in analysis start with the established interfaces from day one. What does this mean? You must start the process by meeting with the right people in the organization. In the best projects, the process is as follows: 1. Executive interface: There needs to be an executive-level supporter of the project. Without such a supporter, you risk not being able to keep the project on schedule. Most important, you need a supporter for the political issues that you may need to handle during the project (discussed in detail later). The executive supporter, sometimes known as a sponsor (JAD reference), should provide a preliminary schedule advising the organization of what is expected and the objectives of the project. The executive supporter should attach a letter to the preliminary schedule and send it to the project team members. The letter must put the importance of the project into perspective. Therefore, it is strongly rec
Read more